Here is just something for fun. This is the basic solution using a reduction algorithm. I have another solution using heuristics to find intricate solutions as well.
Start with creating a table to hold the initial value, like this.
CREATE TABLE dbo.Board (c TINYINT NOT NULL, r TINYINT NOT NULL, d TINYINT NOT NULL);
c is the 1-based column from left to right, r is the 1-based row from bottom to top, and d is the initial value.
Next step is to populate the table with the initial values. You can write a procedure for that using with a table variable, JSON or XML. Is this example I am just showing how to insert the values directly.
TRUNCATE TABLE dbo.Board;
INSERT dbo.Board
VALUES (1, 9, 5),
(1, 8, 6),
(1, 6, 8),
(1, 5, 4),
(1, 4, 7),
(2, 9, 3),
(2, 7, 9),
(2, 3, 6),
(3, 7, 8),
(4, 8, 1),
(4, 5, 8),
(4, 2, 4),
(5, 9, 7),
(5, 8, 9),
(5, 6, 6),
(5, 4, 2),
(5, 2, 1),
(5, 1, 8),
(6, 8, 5),
(6, 5, 3),
(6, 2, 9),
(7, 3, 2),
(8, 7, 6),
(8, 3, 8),
(8, 1, 7),
(9, 6, 3),
(9, 5, 1),
(9, 4, 6),
(9, 2, 5),
(9, 1, 9);
Now you have a board like this
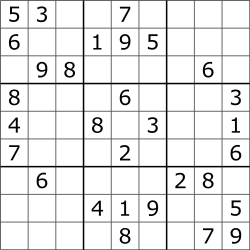
In this basic example I am using a reduction algorithm. To do this, I am inserting all candidate values in the empty cells and then I remove nondeterministic values in an iteration until no more indeterministic values are found.
CREATE OR ALTER PROCEDURE dbo.SodukoSolve
AS
— Prevent unwanted resultsets back to client
SET NOCOUNT ON;
— Local helper variable
DECLARE @Iterations INT = 0;
— Populate candidate digits for nondeterministic cells
WITH cteNumbers(number)
AS (
SELECT number
FROM (
VALUES (1),
(2),
(3),
(4),
(5),
(6),
(7),
(8),
(9)
) AS d(number)
)
MERGE dbo.Board AS tgt
USING (
SELECT c.number AS c,
r.number AS r,
d.number AS d
FROM cteNumbers AS c
CROSS JOIN cteNumbers AS r
CROSS JOIN cteNumbers AS d
) AS src ON src.c = tgt.c
AND src.r = tgt.r
WHEN NOT MATCHED BY TARGET
THEN INSERT (
c,
r,
d
)
VALUES (
src.c,
src.r,
src.d
);
— Compare nondeterministic cells to deterministic cells
WHILE @@ROWCOUNT > 0
BEGIN
SET @Iterations += 1;
WITH cteBoard(c, r, d, n)
AS (
SELECT c,
r,
d,
COUNT(*) OVER (PARTITION BY c, r) AS n
FROM dbo.Board
)
MERGE dbo.Board AS tgt
USING (
SELECT DISTINCT src.c,
src.r,
src.d
FROM cteBoard AS src
LEFT JOIN cteBoard AS hrz ON hrz.c <> src.c
AND hrz.r = src.r
AND hrz.n = 1
LEFT JOIN cteBoard AS vrt ON vrt.c = src.c
AND vrt.r <> src.r
AND vrt.n = 1
LEFT JOIN cteBoard AS sqr ON sqr.c BETWEEN (src.c – 1) / 3 * 3 + 1 AND (src.c – 1) / 3 * 3 + 3
AND sqr.r BETWEEN (src.r – 1) / 3 * 3 + 1 AND (src.r – 1) / 3 * 3 + 3
AND sqr.n = 1
WHERE src.n >= 2
AND src.d IN (hrz.d, vrt.d, sqr.d)
) AS src ON src.c = tgt.c
AND src.r = tgt.r
AND src.d = tgt.d
WHEN MATCHED
THEN DELETE;
END;
— Show solution
IF (SELECT COUNT(*) FROM dbo.Board) = 81
IF @Iterations = 1
PRINT ‘Soduko solved in 1 iteration.’;
ELSE
PRINT CONCAT(‘Soduko solved in ‘, @Iterations, ‘ iterations.‘);
ELSE
PRINT ‘Soduko not solved.‘;
SELECT c,
r,
d
FROM dbo.Board;
Now, you have a simple call to solve your Soduko puzzle. Enjoy!
EXEC dbo.SodukoSolve;



